Sample Paper: Pricing Strategies and Price Discrimination in Oligopolistic Markets
Introduction
Oligopoly is one of the most common market structures. As such, it may be useful to consider how firms set prices in an oligopolistic market as this affects consumers and social welfare. The aim of the paper is to assess pricing strategies and price discrimination in an oligopoly. Key theoretical frameworks are discussed in the context of price competition. It is found that uncertainty surrounding competitors’ behaviour may prevent firms to set prices that maximise total profits of all firms. However, increasing the price above the competitive level is possible through the use of price signalling and price discrimination.
Oligopoly and pricing
Equilibrium in an oligopolistic market
Firms in markets with monopoly, perfect competition, or monopolistic competition may take the levels of market demand and prices as a given (Pindyck and Rubinfeld, 2018). In contrast, firms in an oligopoly have to consider behaviour of their competitors when making a decision regarding output or price. This leads to the concept of Nash equilibrium as a market state in which firms are doing the best they can, given the behaviour of their competitors (Mankiw, 2016). Corporate strategies may be very broad and cover changes in output, prices, advertising, research and development, and investment. Most prominent models of oligopoly focus on two strategic variables, namely price and output.
Cournot model and first-mover advantage in output competition
The Cournot model assumes that firms’ basic strategic variable is output (Dixon, 2001). Firms simultaneously decide on the output level while treating the quantity produced by competitors as fixed. The dependence on the choices of competitors is summarised in reaction curves that show optimal production levels given the output of other firms (Pindyck and Rubinfeld, 2018). The Cournot equilibrium is determined by the intersection of reaction curves. Since this is a Nash equilibrium, no firm would individually prefer to change its output. The model can be adjusted to allow a single firm to make the decision first. The resulting Stackelberg model of oligopoly (Dixon, 2001) provides insight on how it may be advantageous to choose first. Competitors would have to take the increased output level of the first firm as a given and as such produce less.
Bertrand model and pricing competition with differentiated products
In contrast with the Cournout model, the Bertrand model treats price as the basic strategic variable (Dixon, 2001). The model describes price competition with homogenous products. If one firm chooses to decrease its prices, then it will supply the entire market. If the firm increases its prices instead, then it will lose all consumers. The Bertrand-Nash equilibrium occurs when firms set their prices at the level of marginal costs since it would always be advantageous for firms to lower prices in order to capture the whole market (Dixon, 2001). A major disadvantage of the base Bertrand model is that, in a market with homogenous goods, it would be more natural to compete by changing production levels rather than prices (Pindyck and Rubinfeld, 2018). However, the model can be extended to allow for differentiated products so that firms are more likely to compete by setting prices rather than output.
The Nash equilibrium of price competition with differentiated products in a duopoly is illustrated in Figure 1.
Figure 1. Nash equilibrium in prices
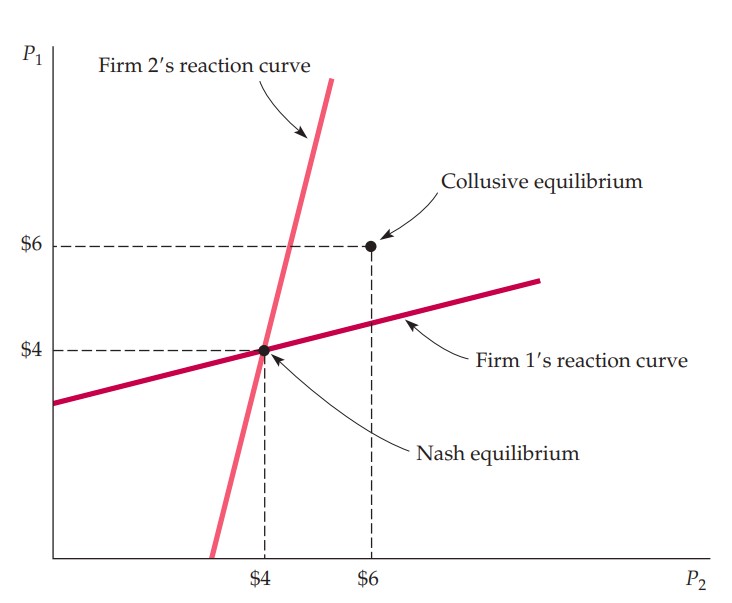
Notes: From Pindyck and Rubinfeld (2018, p.481). and denote prices set by firms 1 and 2, respectively.
Two firms compete by simultaneously setting their prices while taking the price of the other firm as fixed. Firms’ reaction curves show which prices to choose in order to maximise profits given the price of the competitor. The Nash equilibrium occurs at the intersection of the two reaction curves. At the Nash equilibrium, neither firm would individually want to change its price. However, the profits of both firms can be increased if the price is set cooperatively. More precisely, firms may collude to charge the same price determined by maximising total profits of both firms (Dixon, 2001).
While the Stackelberg model suggested a first-mover advantage when the output was used as the strategy variable, the model of price competition in a duopoly implies that the first firm would be at a disadvantage as changing the price first would leave the second firm an undercutting opportunity (Pindyck and Rubinfeld, 2018). As a result, the second firm would be able to capture a larger market share.
Prisoners’ dilemma
The analysis of a simple duopoly pricing model reflects the difference between cooperative and non-cooperative equilibria. The Nash equilibrium is non-cooperative and represents a state where each firm individually maximises its profits. At the same time, firms would earn greater profits at the collusive equilibrium. While colluding may be illegal, firms could attempt to cooperate without explicit collusion by setting their price to the profit-maximising level and hoping that competitors would do the same. Assuming that all firms adopt this behaviour, their total profit would increase compared to the non-cooperative Nash equilibrium.
However, it may be possible for each firm to make more money by setting the price to the Nash equilibrium regardless of the behaviour of its competitors. This problem is similar to the prisoners’ dilemma and suggests that firms would not set their prices at the collusive level as they would earn more by choosing a lower price (Pindyck and Rubinfeld, 2018). Each firm knows that its competitors have the same incentive for undercutting which ultimately discourages passive competition (Dixon, 2001). However, the pricing problem differs from the prisoners’ dilemma as firms are able to adjust prices multiple times and observe the behaviour of their competitors. Reputation and trust created throughout the existence of the oligopoly may lead to more coordination and cooperation.
Pricing strategies
Kinked demand curve model
The prisoners’ dilemma reflects the fragility of a possible implicit collusion between firms in an oligopoly (Pindyck and Rubinfeld, 2018). This may lead to price rigidity as firms are reluctant to quickly adjust prices to changes in demand or costs. In particular, reducing prices as a response to a fall in demand could be misinterpreted by competitors and lead to a price war. Likewise, firms may be discouraged from raising prices as a response to higher demand since they could be unsure whether their competitors would also raise their prices. Several models of pricing can be considered, namely the kinked demand curve model, the dominant firm model, and the collusion model.
The kinked demand curve model is rooted in the price rigidity in oligopolistic markets. The model is illustrated in Figure 2.
Figure 2. The kinked demand curve
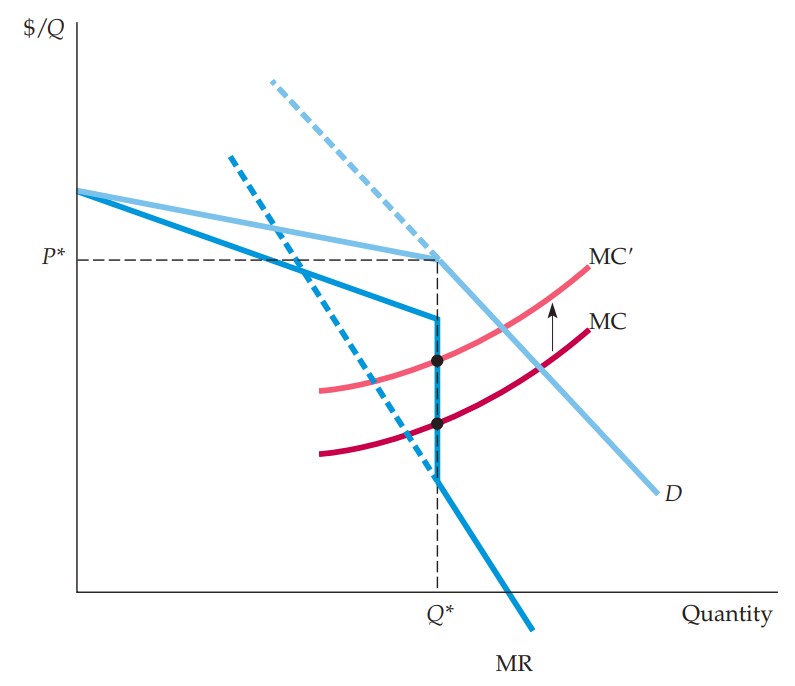
Notes: From Pindyck and Rubinfeld (2018, p.487). and denote prices and output, respectively; is the marginal cost curve; is the demand curve; is the marginal revenue curve.
Firms face demand described by a curve that is kinked at the current price . The curve is more elastic at prices greater than since a firm expects that its competitors would not increase their own prices if it increased its price. Similarly, the curve is less elastic below as it can be expected that firms would follow suite and decrease their prices after one firm lowers its price. Consequently, the marginal revenue curve is discontinuous and as such costs can change from to without a change in price. While the model describes price rigidity, it does not provide a description of the adjustment process.
Dominant firm and price leadership model
The kinked demand curve view suggests why firms may be reluctant to adjust their prices following changes in costs or demand. However, if the firms’ market shares are not comparable, some firms could follow a pricing strategy that maximises their profits without considering uncooperative responses. In particular, an oligopolistic market may have a dominant firm that supplies the majority of the market (Pindyck and Rubinfeld, 2018). Smaller firms could be considered to be in perfect competition while the dominant firm would set prices based solely on individual profit maximisation.
Pricing in an oligopoly with a dominant firm is illustrated in Figure 3.
Figure 3. Price setting by a dominant firm
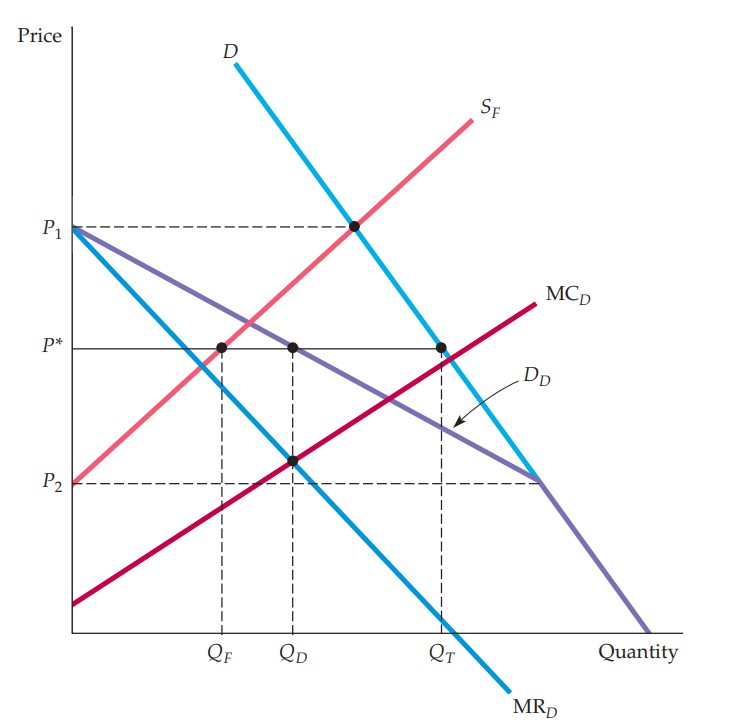
Notes: From Pindyck and Rubinfeld (2018, p.490). and denote prices and output, respectively; is the marginal cost curve; and are the demand and supply curves, respectively; is the marginal revenue curve.
The market demand curve and the supply curve of the smaller firms determine the demand curve of the dominant firm . The dominant firm chooses to produce quantity which equates its marginal revenue with marginal cost . This leads to the price at which smaller firms sell , resulting in total sales of . At price the whole market is supplied by smaller firms while at price the dominant firm supplies the entire market. Thus, in a presence of a dominant firm, the large firm chooses the price to maximise its profits which depends on the supply of smaller firms, while smaller firms take this price as a given and adjust their output accordingly.
Implicit collusion and cartels
The major obstacle to implicit collusion is for all firms to agree on the cooperative price without explicit discussion (Pindyck and Rubinfeld, 2018). As such, the pricing strategy of some firms may involve price signalling which may take the form of a public announcement of a price increase. The firm would expect that its competitors follow suit in order to attain a cooperative equilibrium with higher total profits for all firms. Price signalling may result in a single firm being recognised as a leader that announces price hikes first. Thus, firms solve the coordination problem of the prisoners’ dilemma by agreeing on waiting for price changes of a single firm.
Unlike implicit collusion, cartels explicitly agree on setting prices cooperatively. Relatively inelastic market demand and large cartel size may allow producers to increase prices above the competitive equilibrium (Mankiw, 2016). The pricing strategy is identical to the dominant firm model as the cartel’s demand would be determined by the difference between total demand and demand of non-cartel producers. Setting the output to the profit-maximising quantity that equates marginal cost and marginal revenue would result in a price that is higher compared to an oligopoly with no cartelised producers.
Price discrimination
Firms in an oligopoly may choose to adjust their prices to specific customers even if the production costs for these customers are the same (Liu and Serfes, 2004). This practice of price discrimination requires the firm to have some market power and the ability to sort customers (Corts, 1998; Mankiw, 2016) as well as the ability to prevent resales (Chen, 1999). Several types of price discrimination can be distinguished (Varian, 1989). First-degree price discrimination occurs when the seller charges a different price for each unit matching the maximum willingness-to-pay for that unit. It may take the form of ‘take-it-or-leave-it’ offers and two-part tariffs. Second-degree price discrimination describes price schedule that depends on the number of units bought. Quantity discounts constitute the most widely-used form of this practice. Third-degree price discrimination represents different purchasers having different price schedules. This type of discrimination may take the form of airline fares, movie tickets, financial aid, and discount coupons (Holmes, 1989), and constitutes the most common form of price discrimination (Varian, 1989; Dastidar, 2006).
Price discrimination relies on the difference in price elasticities of consumers (Bakó and Kálecz-Simon, 2012; Mankiw, 2016). This difference depends on the form of consumer heterogeneity and consumer preferences (Kutlu, 2012). Third-degree price discrimination is. Firms may use purchase history to reveal consumer price sensitivities (Chen, 2005). Notably, the demand of past consumers could be more inelastic due to switching costs. This results in differentiating otherwise homogenous goods (Dockner and Jørgensen, 1988). Another example is purchase history revealing a consumer’s strong preference for a specific product (Armstrong, 2006). As such, firms in an oligopoly may adopt pricing strategies that selectively reduce prices for past consumers of their competitors (Asplund et al., 2008; Hazledine, 2010). In the context of cooperative behaviour, firms may implicitly agree to restrict price discrimination in order to increase effective price and profits (Stole, 2007).
Conclusion
The aim of the paper was to consider pricing strategies and price discrimination in an oligopolistic market. It was found that a cooperative equilibrium would result in greater profits for all firms. At the same time, firms may feel reluctant to adjust prices in fear of uncooperative behaviour such as undercutting and price wars. Increasing profits is possible through the use of price signalling, cartelising, and price discrimination practices such as quantity discounts, discount coupons, and selective pricing for customers of competitive firms.
References
Armstrong, M. (2006). Recent developments in the economics of price discrimination. In: Blundell, R., Newey, W. K., and Persson, T. (Eds.) Advances in Economics and Econometrics: Theory and Applications: Ninth World Congress: volume II. Cambridge: Cambridge University Press, pp.97-141.
Asplund, M., Eriksson, R., and Strand, N. (2008). Price discrimination in oligopoly: evidence from regional newspapers. The Journal of Industrial Economics, 56(2), pp.333-346.
Bakó, B., and Kálecz-Simon, A. (2012). Price discrimination in asymmetric Cournot oligopoly. Economics Letters, 116(3), pp.301-303.
Chen, Y. (1999). Oligopoly price discrimination and resale price maintenance. The RAND Journal of Economics, 30(3), pp.441-455.
Chen, Y. (2005). Oligopoly price discrimination by purchase history. In Bergman, M. (Ed.) The Pros and Cons of Price Discrimination. Stockholm: Konkurrensverket, pp.101-130.
Corts, K. S. (1998). Third-degree price discrimination in oligopoly: all-out competition and strategic commitment. The RAND Journal of Economics, 29(2), pp.306-323.
Dastidar, K. G. (2006). On Third‐Degree Price Discrimination in Oligopoly. The Manchester School, 74(2), pp.231-249.
Dixon, H. W. (2001). Surfing Economics: Essays for the Inquiring Economist. Basingstoke: Palgrave.
Dockner, E., and Jørgensen, S. (1988). Optimal pricing strategies for new products in dynamic oligopolies. Marketing Science, 7(4), pp.315-334.
Hazledine, T. (2010). Oligopoly price discrimination with many prices. Economics Letters, 109(3), pp.150-153.
Holmes, T. J. (1989). The effects of third-degree price discrimination in oligopoly. The American Economic Review, 79(1), pp.244-250.
Kutlu, L. (2012). Price discrimination in Cournot competition. Economics Letters, 117(3), pp.540-543.
Liu, Q., and Serfes, K. (2004). Quality of information and oligopolistic price discrimination. Journal of Economics and Management Strategy, 13(4), pp.671-702.
Mankiw, N. G. (2016). Principles of Economics. Boston: Cengage Learning.
Pindyck, R. S., and Rubinfeld, D. L. (2018). Microeconomics. Harlow: Pearson Education.
Stole, L. A. (2007). Price discrimination and competition. In Schmalensee, R. and Willig, R. (Eds.) Handbook of Industrial Organisation: Volume 3. London: Elsevier, pp.2221-2299.
Varian, H. (1989). Price discrimination. In Schmalensee, R. and Willig, R. (Eds.) Handbook of Industrial Organisation: Volume 1. London: Elsevier, pp.597-654.

